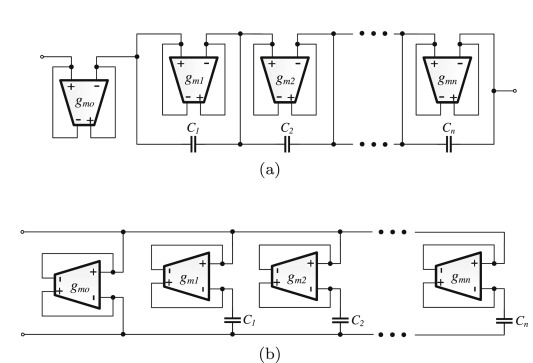
Realizations of simple fractional-order capacitor emulators with electronically-tunable capacitance
A novel resistorless topology for implementing fractional-order capacitor emulators, based on the employment of Operational Transconductance Amplifiers (OTAs) as active elements, is presented in this paper. The benefits of this topology are its simplicity in terms of component count, compared to other existing topologies in the literature, in addition to its electronic tunability. The performance of the presented topology is evaluated using Cadence and the 0.35 μm CMOS process Design Kit from Austria Mikro Systeme. Experimental results using commercial OTA chips are also provided, where the
Fractional order oscillators based on operational transresistance amplifiers
In this paper, a general analysis of the fractional order operational transresistance amplifiers (OTRA) based oscillator is presented and validated through eight different circuits which represent two classifications according to the number of OTRAs. The general analytical formulas of the oscillation frequency, condition as well as the phase difference are illustrated for each case and summarized in tables. One of the advantages of the fractional-order circuit is the extra degrees of freedom added from the fractional-order parameters. Moreover different special cases {α = β ≢ 1, β ≢ α = 1, α ≢
Experimental verification of triple lobes generation in fractional memristive circuits
Recently, the triple-lobe behavior is found in the I-V characteristics of some memristive devices generating another non-zero pinchoff point. In this paper, a flux-controlled memristive model is developed to generate the triple-lobe behavior (double pinchoff points) based on a fractional second-order model. The conditions for observing triple lobes are derived besides the coordinates of the pinchoff points. Different scenarios have been considered by changing the model parameters and fractional order. Furthermore, the minimum and maximum achievable conductances are analyzed and mathematically
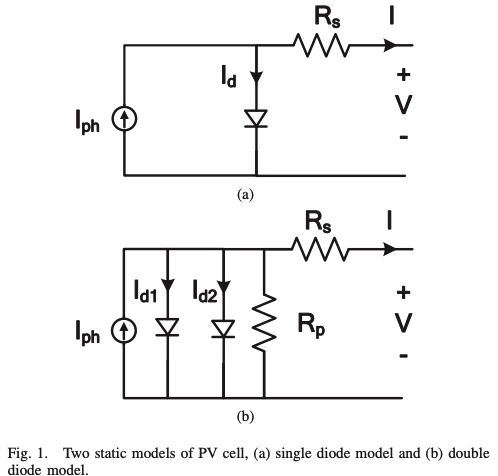
A fractional-order dynamic PV model
A dynamic model of Photo-Voltaic (PV) solar module is important when it is utilized in conjunction with switching circuits and in grid connected applications. In this paper, a fractional-order dynamical model of a PV source is introduced. The model includes both a fractional series inductor and a parallel capacitor which are in general of two different orders allowing for extra degrees of modeling freedom. An expression for the load current is derived and the step response is investigated for different orders. It is found that the nature of the connections has a dominant effect on the response
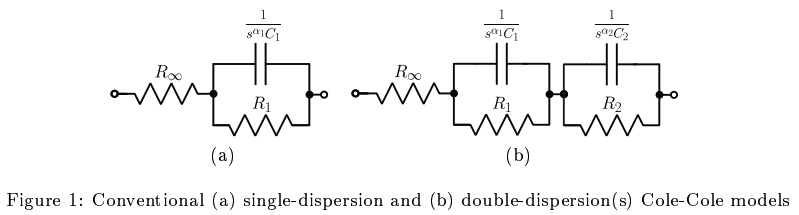
A generic impedance modeling technique
In this work, a generic impedance modeling technique is proposed. The technique is able to identify a circuit model that is most suitable for fitting measured impedance magnitude data using a genetic algorithm solver as well as the optimum circuit model parameters. Experimentally measured and simulated data sets with different noise levels are used to validate the technique. © 2020 Elsevier GmbH
Resistorless memristor based oscillator
This paper introduces the replacement of four and six resistors with four and six memristors at the same time for the modified single input Op-Amps oscillator. The full independency between the oscillation condition and the oscillation frequency facilitates the study. Mathematical analysis is provided for the double replacement of resistors with memristors. The whole range of operation of the memristor is taken in consideration and examined for all kind of replacements. Also, the poles of the system are presented while the existence of two, four and six memristors. © 2014 IEEE.
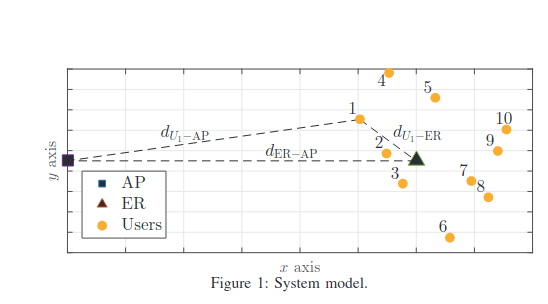
Non-Orthogonal Multiple Access schemes in Wireless Powered Communication Networks
We characterize time and power allocations to optimize the sum-throughput of a Wireless Powered Communication Network (WPCN) with Non-Orthogonal Multiple Access (NOMA). In our setup, an Energy Rich (ER) source broadcasts wireless energy to several devices, which use it to simultaneously transmit data to an Access Point (AP) on the uplink. Differently from most prior works, in this paper we consider a generic scenario, in which the ER and AP do not coincide, i.e., are two separate entities. We study two NOMA decoding schemes, namely Low Complexity Decoding (LCD) and Successive Interference
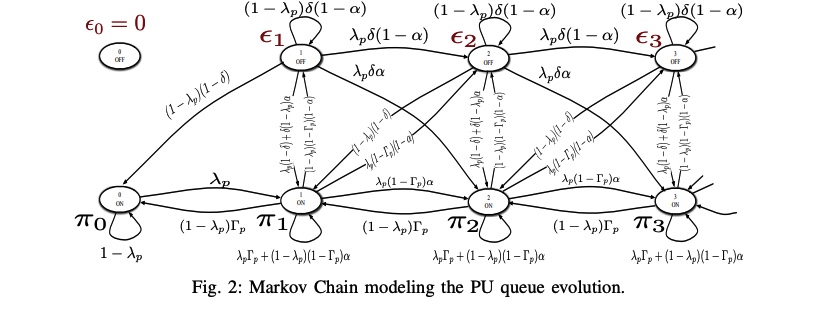
A feedback-soft sensing-based cognitive access scheme with feedback erasures
In this paper, we examine a cognitive spectrum access scheme in which a secondary user exploits the primary feedback information. We consider an overlay model in which the secondary user accesses the channel by certain access probabilities that are function of the spectrum sensing metric. In setting our problem, we assume that the secondary user can receive the primary link's feedback automatic repeat request (ARQ), but through an erasure channel. This means that the primary feedback may either be received correctly or is erased with a certain erasure probability. We study the cognitive radio
Full-duplex cooperative cognitive radio networks
In this paper, we study the impact of a full-duplex secondary node on a cognitive cooperative network with Multipacket Reception (MPR) capabilities at the receivers. Motivated by recent schemes that make full-duplex communication feasible, we study a model with one primary and one secondary transmitter-receiver pair, where the secondary transmitter is able to relay primary unsuccessful packets. Cooperation between primary and secondary users has been previously shown to be beneficial for the primary and the secondary users in terms of stable throughput. Our model assumes an imperfect full
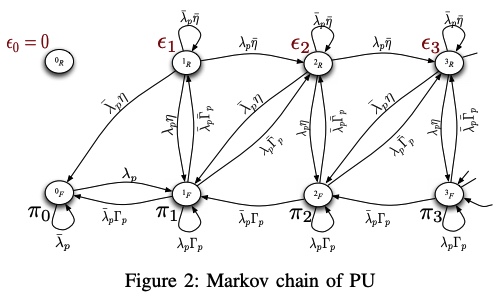
A feedback-based access scheme for cognitive-relaying networks
In this paper, we consider a cognitive relaying network in which the secondary user accesses the channel with a certain access probability that depends on the feedback information sent by the primary destination. In addition, the secondary user is granted relaying capabilities by which it can relay primary traffic that was unsuccessfully transmitted by the primary user. We show that this proposed scheme enhances the performance of the secondary user as well as the primary user, while the QoS requirements of the primary user is unviolated. The secondary user can avoid sure collisions with the
Pagination
- Previous page ‹‹
- Page 33
- Next page ››
