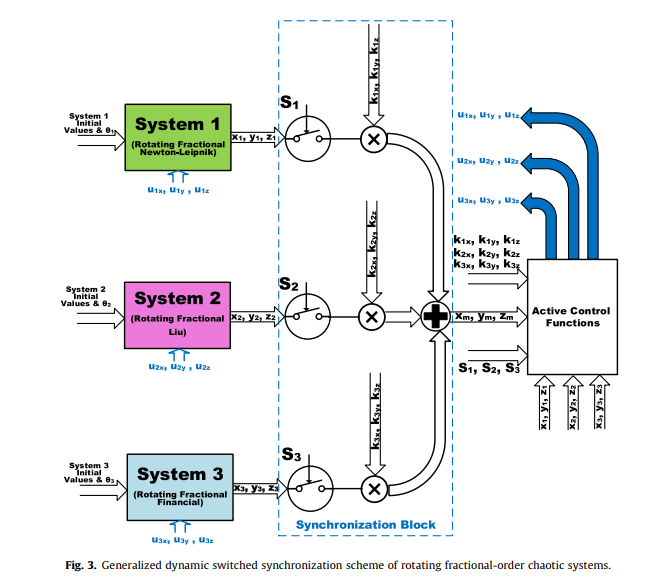
Generalized switched synchronization and dependent image encryption using dynamically rotating fractional-order chaotic systems
This paper presents a generalization, attractor control and multi-scroll generation method for fractional-order chaotic systems through rotation transformation. A novel synchronization-dependent colored image encryption and secure communication scheme is also proposed. The systems with dynamic rotation angle fit successfully in a generalized dynamic switched synchronization scheme. Dynamic control switches specify whether the system acts as a master or slave. Dynamic scaling factors determine whether the master is a single system or a combination of two or more systems. Simulation results
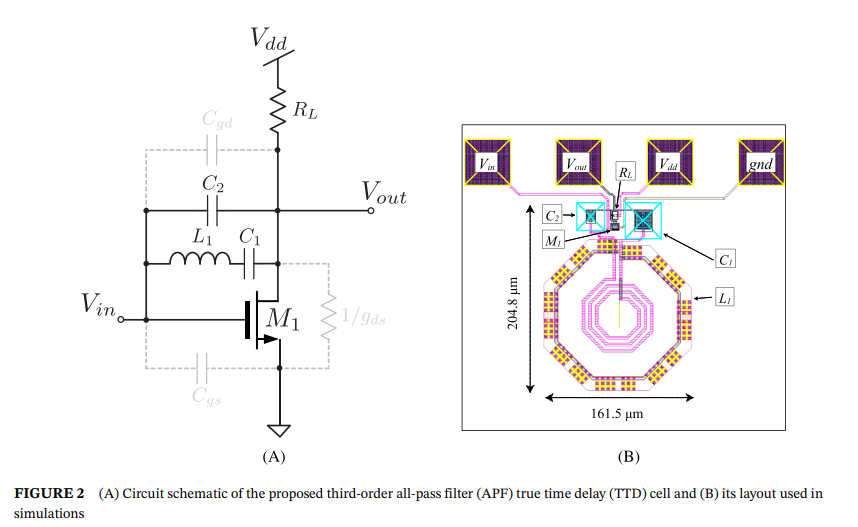
Wideband third-order single-transistor all-pass filter
In this letter, a third-order wideband voltage-mode all-pass filter (APF) is proposed for application as a true time delay (TTD) cell. The advantages of designing a single-stage higher order filter over cascading several lower order stages are illustrated. The proposed APF circuit is based on a single metal-oxide-semiconductor (MOS) transistor and is canonical because it requires one resistor, one inductor, and two capacitors. To the best of the authors' knowledge, this is the first single-transistor third-order APF circuit to be reported in the literature. The operation of the proposed APF is
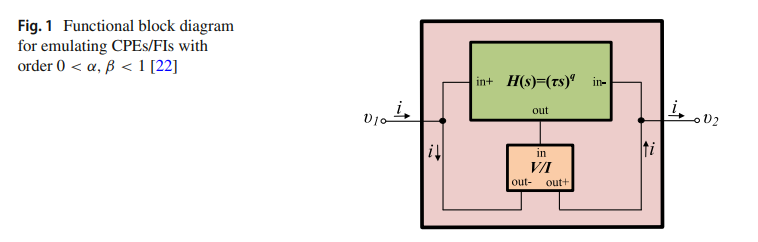
Generalized Fully Adjustable Structure for Emulating Fractional-Order Capacitors and Inductors of Orders less than Two
A novel scheme suitable for the emulation of fractional-order capacitors and inductors of any order less than 2 is presented in this work. Classically, fractional-order impedances are characterized in the frequency domain by a fractional-order Laplacian of the form s± α with an order 0 < α< 1. The ideal inductor and capacitor correspond, respectively, to setting α= ± 1. In the range 1 < α< 2 , fractional-order impedances can still be obtained before turning into a Frequency- Dependent Negative Resistor (FDNR) at α= ± 2. Here, we propose an electronically tunable fractional-order impedance
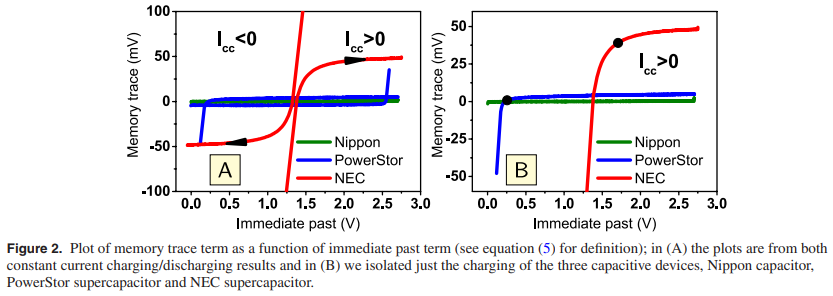
Quantification of memory in fractional-order capacitors
In this study we quantify and interpret the inherent memory in fractional-order capacitors when subjected to constant current charging/discharging waveforms. This is done via a finite difference approximation of the fractional order rate equation I(t) = Cαdαv(t)/dtα (0 le; α ≤ 1) relating current to voltage in these devices. It is found that as the fractional exponent α decreases, the weight of the voltage memory trace that results from the contribution of past voltage activity increases, and thus the measured response of the device at any time is increasingly correlated to its past. Ideal
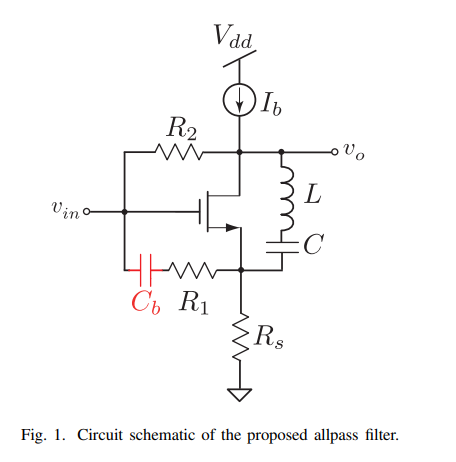
8-GHz low-power voltage-mode second-order allpass filter in 65-nm CMOS
In this paper, a CMOS wide-band low-power second-order voltage-mode allpass filter design is proposed as a true time delay element. The proposed allpass filter core design consists of a single transistor, three resistors, one capacitor and one inductor. As a time delay element, the proposed circuit exhibits a group delay of 34 ps within a bandwidth of 8 GHz while consuming only 926 μW from a 1-V supply voltage. The proposed filter was designed in 65-nm CMOS technology and verified through post-layout simulation results. © 2019 IEEE.
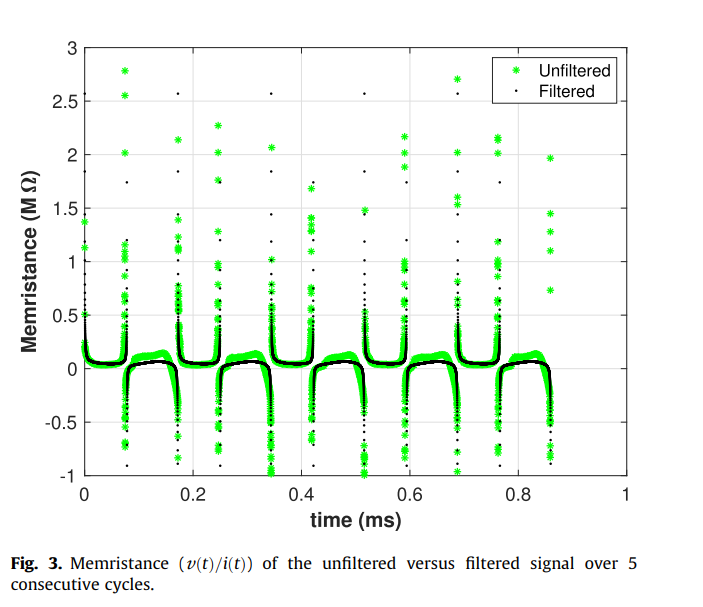
On the mechanism of creating pinched hysteresis loops using a commercial memristor device
In this short communication we analyze the impact of signal harmonics on the formation of the pinched hysteresis loop using a commercial memristor device. We show that by using only the fundamental frequency and the second harmonic components, extracted from the measured electrical current signal, a distortion-less pinched hysteresis loop is re-created. This loop is then used to simulate memristor-based AND/OR gates without any loss in digital functionality. This verifies that the generation of a pinched hysteresis loop requires a nonlinear frequency doubling mechanism to create a second
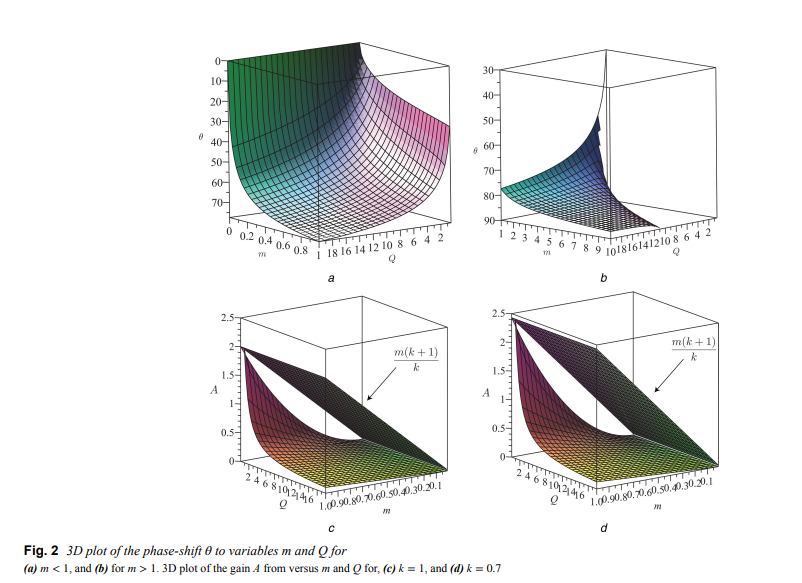
Third-order tunable-phase asymmetric crosscoupled oscillator
Here, the authors show that an asymmetric cross-coupled oscillator can be used to achieve independent-phase tunable outputs. In particular, a third-order cross-coupled oscillator, with non-balanced loads, is studied and expressions for its start-up condition, oscillation frequency, phase-shift between its two outputs as well as their amplitude ratio are derived. From these expressions, it is found that independent tuning of these design specifications is possible and a voltage-controlled phasetunable oscillator can be achieved. As a consequence of the non-balanced loads, the tail biasing
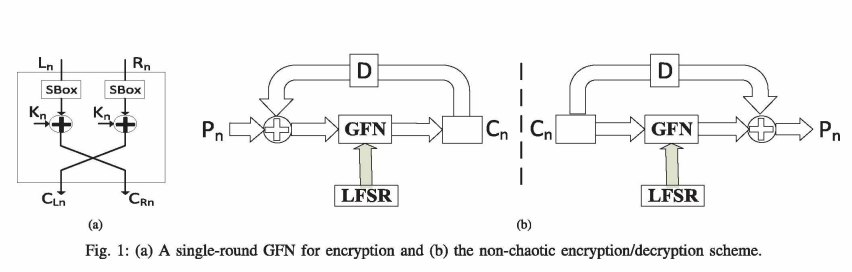
Security and Efficiency of Feistel Networks Versus Discrete Chaos for Lightweight Speech Encryption
This paper compares examples of non-chaotic and chaotic ciphers from the viewpoint of their suitability for speech encryption, especially in real-time and lightweight cipher systems. The non-chaotic encryption scheme depends on a modified Generalized Feistel Network (GFN), Linear Feedback Shift Register (LFSR) and Substitution Boxes (S-Boxes). The chaotic encryption scheme utilizes a generalized modified tent map with multiple modes of operation. The security and efficiency of both schemes are analyzed using the perceptual tests: time waveform and spectrogram; the statistical tests: histogram
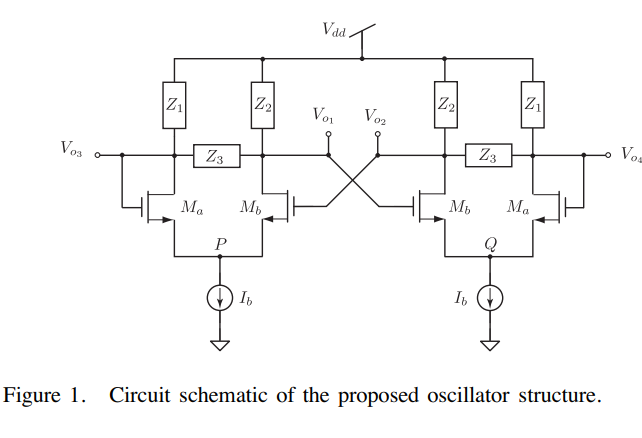
On a class of quadrature phase oscillators using differential pairs
A new class of quadrature phase oscillators based on cross-coupled differential pairs is introduced. This class contains eight possible circuits which produce four output voltages with phase differences of ±π or ±π/2, depending on the choice of output node, and does not require balanced differential-pair loads. Phase error analysis is provided along with experimental and simulation results using discrete MOS and BJT transistors as a proof of concept. © 2018 IEEE
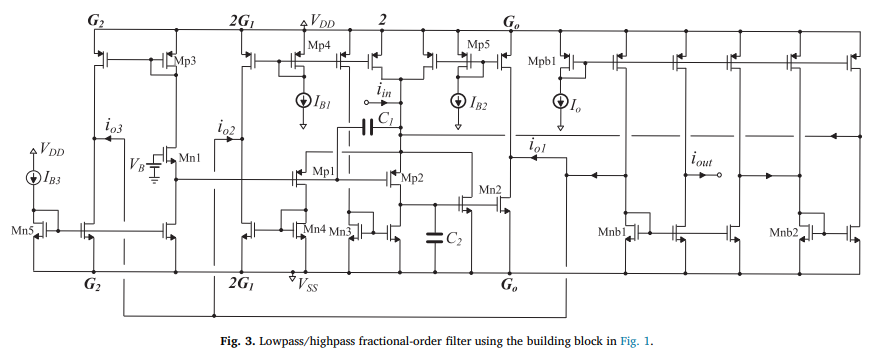
Design and application examples of CMOS fractional-order differentiators and integrators
Reduced complexity CMOS fractional-order differentiator and integrator building blocks are introduced in this work, based on 2 nd -order integer-order transfer function approximations. These blocks are then used for implementing fractional-order filters as well as a Leaky-Integrate-and-Fire Mihalas-Niebur neuron model. Cascading 1 st and 2 nd -order blocks to obtain 5 th -order integer-order transfer functions, improved bandwidth of approximation accuracy is achieved. Furthermore, the realization of fractional-order capacitor and inductor emulators is demonstrated. © 2018 Elsevier Ltd
Pagination
- Previous page ‹‹
- Page 24
- Next page ››
