Fractional order integrator/differentiator: FPGA implementation and FOPID controller application
This paper introduces two FPGA based design approaches of the fractional order integrator and differentiator using Grünwald Letnikov (GL) definition where fixed window and linear approximation approaches are considered. The main advantage of the linear approximation method is that it reduces the huge memory of the fractional order systems. One of the top applications of fractional calculus is the fractional order Proportional Integral Derivative (FOPID) controller. It has gained a great attention in academic studies and in industrial applications. The proposed approaches have been used as
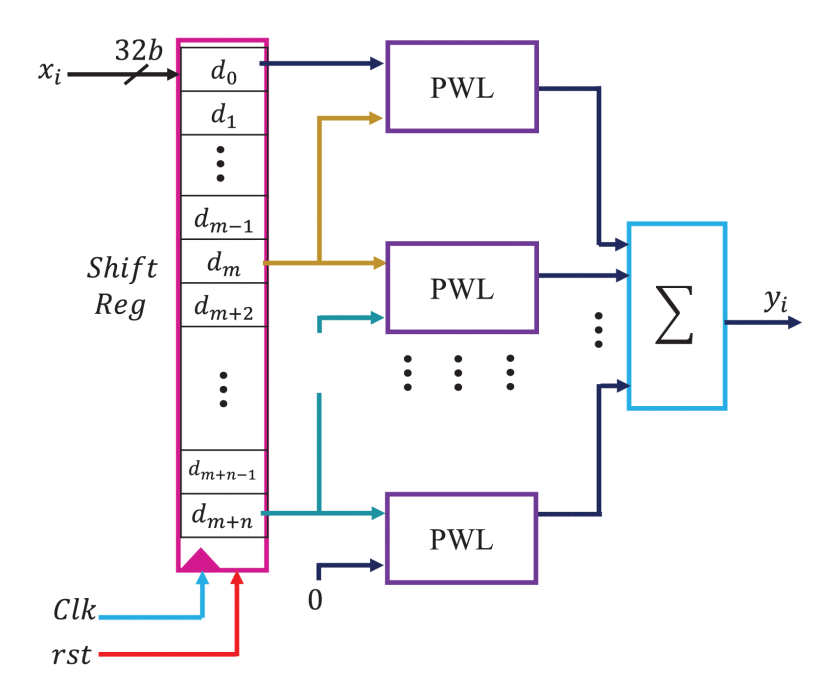
FPGA Implementation of the Fractional Order Integrator/Differentiator: Two Approaches and Applications
Exploring the use of fractional calculus is essential for it to be used properly in various applications. Implementing the fractional operator Dα in FPGA is an important research topic in fractional calculus; in the literature, only a few FPGA implementations have been proposed due to the memory dependence of the fractional order systems. In this paper, FPGA implementations of fractional order integrator/differentiator based on the Grünwald-Letnikov (GL) operator are proposed. Two algorithms are developed based on look-up table and quadratic and piece-wise linear approximation approaches to
FPGA implementation of fractional-order integrator and differentiator based on Grünwald Letnikov's definition
The fractional-order derivative and integral of Grünwald Letnikov's definition are implemented based on FPGA for different fractional orders. A new algorithm is proposed to implement the GL integral based on linear approximation approach, where the memory dependency of the fractional order systems is eliminated. Moreover, the linear approximation design shows an improvement of 91% and 92% in the error and the mean percentage error compared with prior art. The proposed approach has been designed and implemented based on Verilog Hardware Description Language (HDL) and realized on Nexys 4 Artix-7
Fractional-order synchronization of two neurons using Fitzhugh-Nagumo neuron model
This paper studies the synchronization of two coupled neurons using Fitzhugh-Nagumo model in the fractional-order domain. In general, studying systems in the fractional-order domain provides a wider scope view of their behavior. When the neuron is generalized into the fractional-order domain, the normal behaviors displayed in the integer case change. Furthermore, two neurons display various synchronization patterns. The neurons' fractional-order system is solved using non-standard finite difference scheme together with Grunwald-Letnikov discretization. © 2016 IEEE.
Fractional-order impedance transformation based on three port mutators
Due to the importance of the mutators for active circuit realizations, this paper investigates different three port mutator circuits that can be used to implement a floating impedance. The analytical equations that govern the proposed circuits as well as the necessary conditions under different configurations are introduced to realize positive and negative impedances. The proposed circuits are based on second generation current conveyors (CCII) and/or transconductance Amplifier (TA). Moreover, the fractional-order impedance transformation using these mutators are investigated showing the

Simple floating voltage-controlled memductor emulator for analog applications
The topic of memristive circuits is a novel topic in circuit theory that has become of great importance due to its unique behavior which is useful in different applications. But since there is a lack of memristor samples, a memristor emulator is used instead of a solid state memristor. In this paper, a new simple floating voltage-controlled memductor emulator is introduced which is implemented using commercial off the shelf (COTS) realization. The mathematical modeling of the proposed circuit is derived to match the theoretical model. The proposed circuit is tested experimentally using
Rectangular waveguides in the fractional-order domain
This work introduces Maxwell's equations in their time domain fractional derivatives form. Some special cases of fractional order wave equations are shown. Studying the effect of fractional-order derivatives with respect to time on the generalized analysis and fundamentals of the rectangular waveguide is the main focus of this work. The effect of the fractional-order parameters on the waveguide properties is shown. Some of these properties are cutoff frequency and attenuation that are no longer fixed but controllable by the fractional parameters. Also, the intrinsic impedance is shown to be
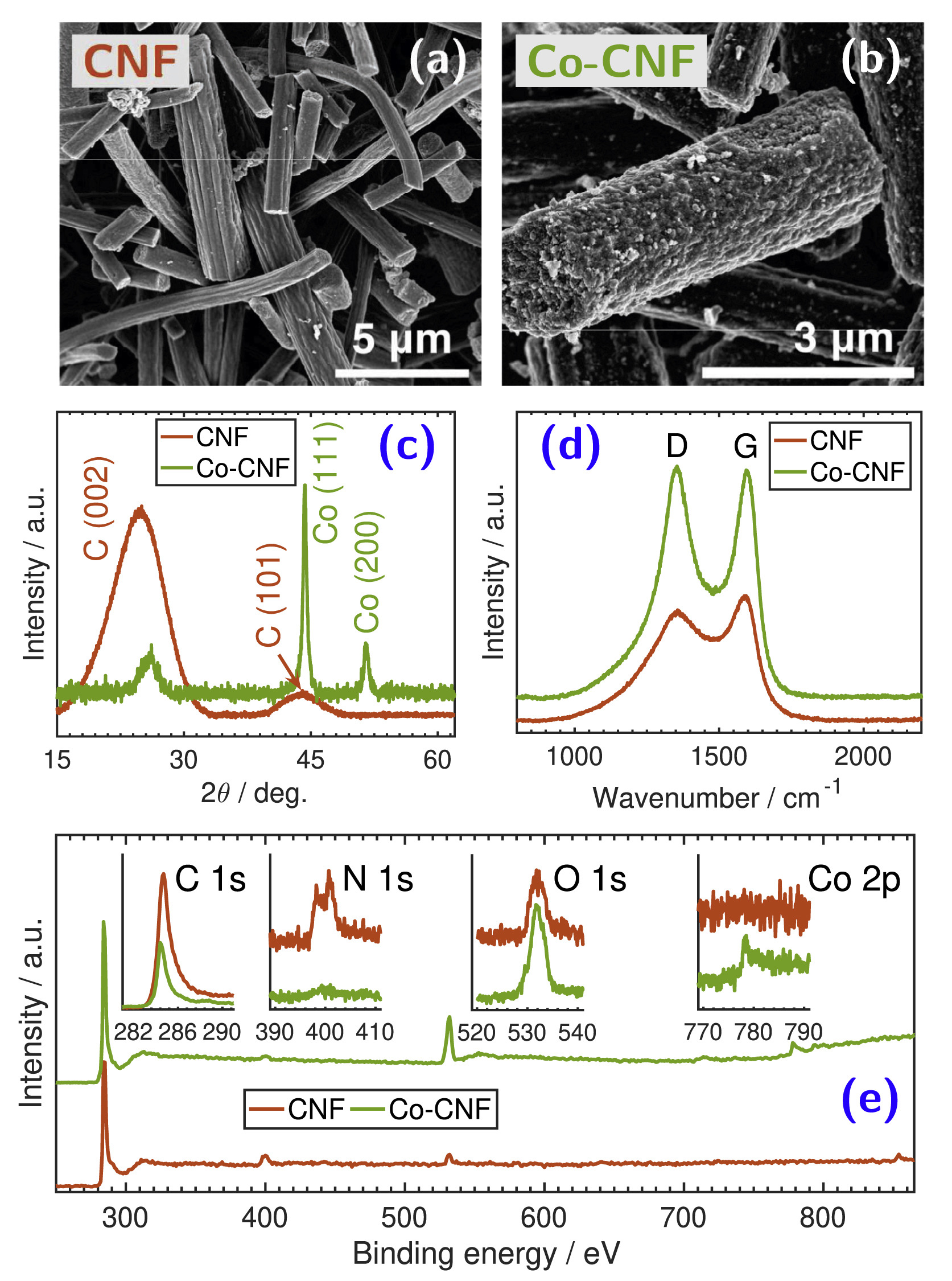
Modulating the energy storage of supercapacitors by mixing close-to-ideal and far-from-ideal capacitive carbon nanofibers
The quest for high performance supercapacitors from the energy-power point of view is commonly addressed from the constituting electrode materials and/or the electrolyte. Carbon-based double-layer capacitors are known for their high power density, whereas pseudocapacitors which use transition metal oxides/nitrides/sulfides or conductive polymers are known for their high energy density. In this work we show that one can modulate the energy storage capability of supercapacitors by mixing at preset ratios two types of carbon materials having two different energy storage capabilities. The time
Fractional-order mutual inductance: Analysis and design
This paper introduces for the first time the generalized concept of the mutual inductance in the fractional-order domain where the symmetrical and unsymmetrical behaviors of the fractional-order mutual inductance are studied. To use the fractional mutual inductance in circuit design and simulation, an equivalent circuit is presented with its different conditions of operation. Also, simulations for the impedance matrix parameters of the fractional mutual inductance equivalent circuit using Advanced Design System and MATLAB are illustrated. The Advanced Design System and MATLAB simulations of
FPGA realizations of high-speed switching-type chaotic oscillators using compact VHDL codes
This paper introduces high-speed FPGA implementations of two different chaotic systems that rely on a switching-type nonlinearity. In particular, the single-switch Jerk system and the two-wing butterfly system (previously implemented only in analog form) are realized on a modular FPGA platform. For each system, two different hardware architectures are described: a parameters-independent architecture and a customized one with fixed parameters that utilizes less FPGA resources and thus has high throughput with the minimum number of clock cycles. Experimental results show that the parameters
Pagination
- Previous page ‹‹
- Page 30
- Next page ››
