Single active element implementation of fractional-order differentiators and integrators
A novel topology for implementing fractional-order differentiator and integrator transfer functions is presented in this paper. This topology is based on the employment of a second generation Current Conveyor with EXtra inputs (EX-CCII), passive resistors, and fractional-order capacitors. The main benefit offered by this implementation is that both fractional-order differentiator and integrator transfer functions are simultaneously available at different output terminals, and that their frequency characteristics can be orthogonally adjusted without disturbing each other. With only one EX-CCII
Fractional Order Sallen–Key and KHN Filters: Stability and Poles Allocation
This paper presents the analysis for allocating the system poles and hence controlling the system stability for KHN and Sallen–Key fractional order filters. The stability analysis and stability contours for two different fractional order transfer functions with two different fractional order elements are presented. The effect of the transfer function parameters on the singularities of the system is demonstrated where the number of poles becomes dependent on the transfer function parameters as well as the fractional orders. Numerical, circuit simulation, and experimental work are used in the
Experimental demonstration of fractional-order oscillators of orders 2.6 and 2.7
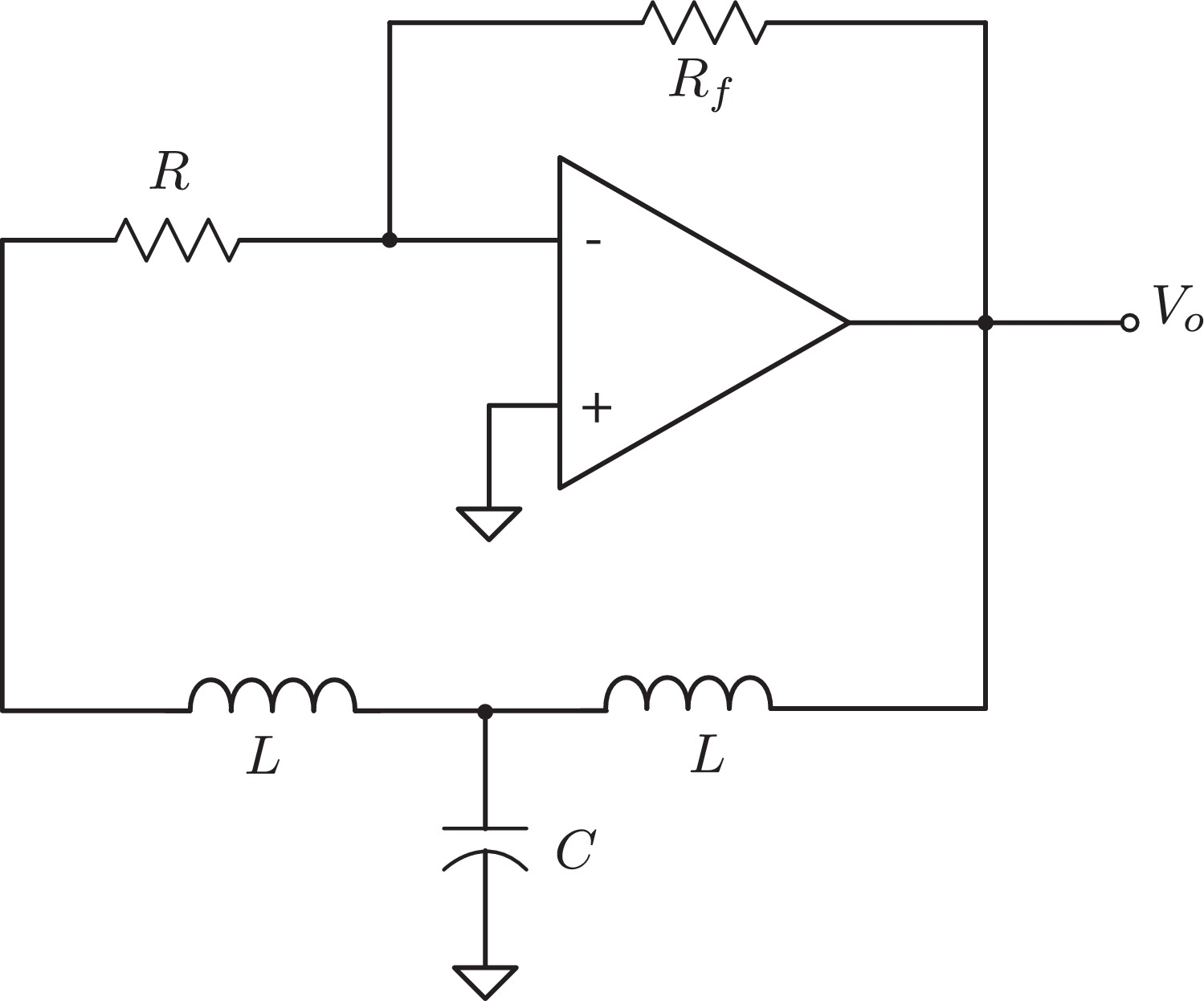
The purpose of this work is to provide an experimental demonstration for the development of sinusoidal oscillations in a fractional-order Hartley-like oscillator. Solid-state fractional-order electric double-layer capacitors were first fabricated using graphene-percolated P(VDF-TrFE-CFE) composite structure, and then characterized by using electrochemical impedance spectroscopy. The devices exhibit the fractional orders of 0.6 and 0.74 respectively (using the model Zc=Rs+1/(jω)αCα), with the corresponding pseudocapacitances of approximately 93nFsec−0.4 and 1.5nFsec−0.26 over the frequency
Novel Double-Dispersion Models Based on Power-Law Filters
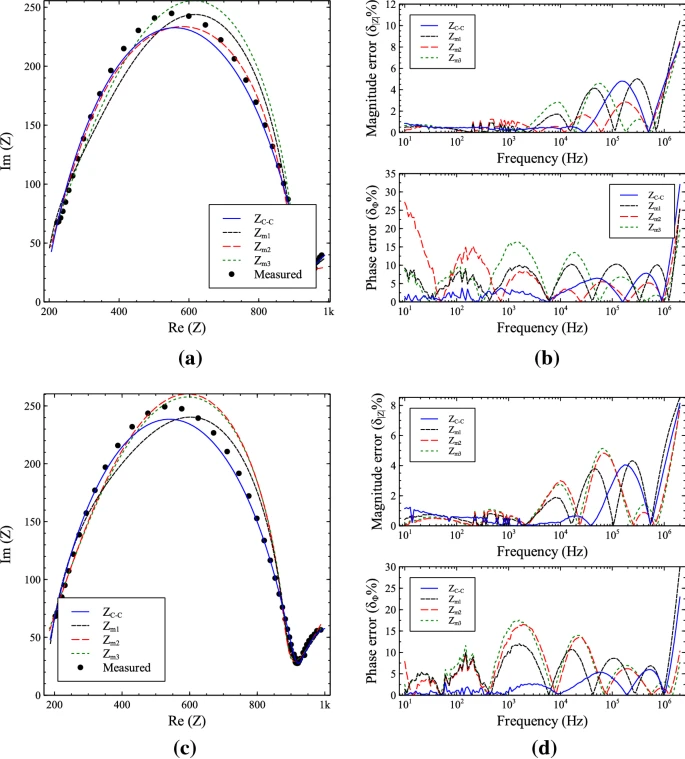
Novel double-dispersion models based on power-law filters are introduced in this work. These models are based on standard first-order and/or second-order low-pass filter transfer functions (denoted as mother functions) and do not require the employment of the fractional-order Laplacian operator. An attractive benefit, from the flexibility point of view, is that the number of parameters, which must be determined via optimization routines, depends on the selected combinations of mother filters. The validity of the proposed models is verified through fitting experimental bio-impedance data of
Simple MOS-based circuit designed to show pinched hysteresis behavior
We propose and validate a simple 3-transistor MOS circuit that shows an all-positive pinched hysteresis behavior. Complete analysis of the circuit is provided along with experimental results using a commercial CMOS transistor array. Copyright © 2018 John Wiley & Sons, Ltd.
Memristor and inverse memristor: Modeling, implementation and experiments
Pinched hysteresis is considered to be a signature of the existence of memristive behavior. However, this is not completely accurate. In this chapter, we are discussing a general equation taking into consideration all possible cases to model all known elements including memristor. Based on this equation, it is found that an opposite behavior to the memristor can exist in a nonlinear inductor or a nonlinear capacitor (both with quadratic nonlinearity) or a derivative-controlled nonlinear resistor/transconductor which we refer to as the inverse memristor. We discuss the behavior of this new
Boundary Dynamics of Memcapacitor in Voltage-Excited Circuits and Relaxation Oscillators
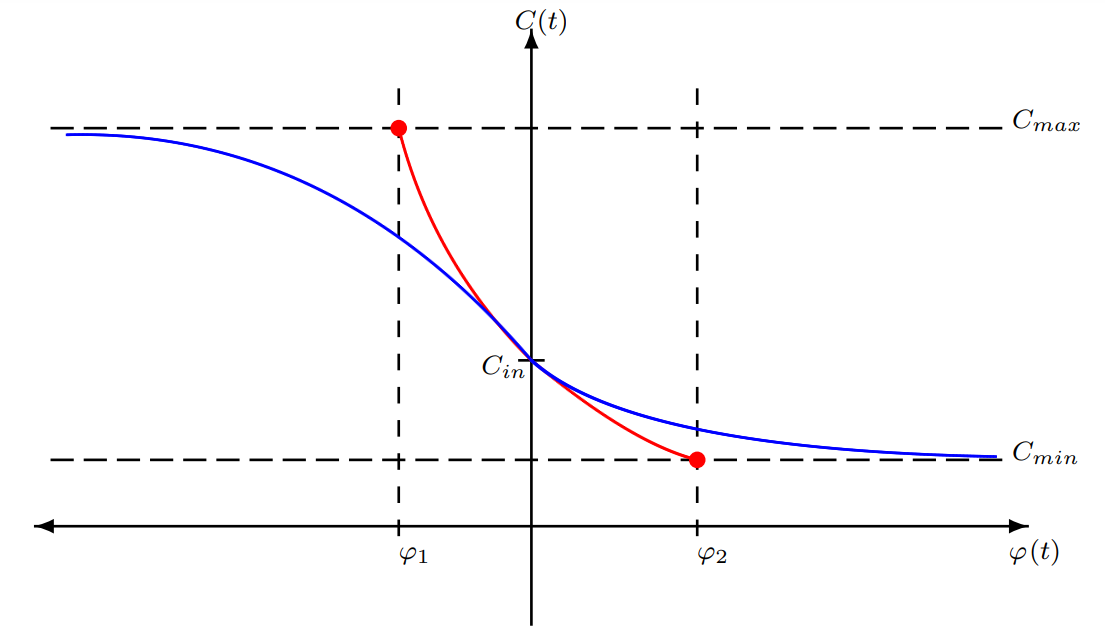
This paper discusses the boundary dynamics of the charge-controlled memcapacitor for Joglekar’s window function that describes the nonlinearities of the memcapacitor’s boundaries. A closed form solution for the memcapacitance is introduced for general doping factor (Formula presented.)p. The derived formulas are used to predict the behavior of the memcapacitor under different voltage excitation sources showing a great matching with the circuit simulations. The effect of the doping factor (Formula presented.) on the time domain response of the memcapacitor has been studied as compared to the
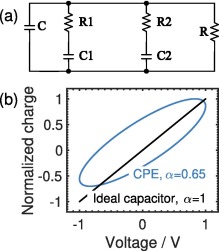
Nonlinear charge-voltage relationship in constant phase element
The constant phase element (CPE) or fractional-order capacitor is an electrical device that has an impedance of the form Z(s)=1/Cαsα, where Cα is the CPE parameter and α is a fractional dispersion coefficient of values between 0 and 1. Here we show that in the time-domain the classical linear charge-voltage relationship of ideal capacitors, q=C·v, is not valid for CPEs. In fact the relationship is nonlinear and can be expressed as q=C(v;Cα,α)·v. We verify our findings using (i) circuit simulations of an integer-order emulator of a CPE, and (ii) experimental results from a commercial
FPGA Implementation of Delayed Fractional-Order Financial Chaotic System
This paper proposes digital design and realization on Field-Programmable Gate Array (FPGA) of the Fractional-order (FO) delayed financial chaotic system. The system is solved numerically using the approximated Grünwald-Letnikov (GL) method. For the purpose of FPGA realization, the short memory principle and an approximate GL with limited window size are utilized. Lookup Tables (LUTs) are employed to store the required state values in order to compute the delayed terms. The proposed digital design is implemented on Artix-7 FPGA platform XC7A100T and realized experimentally on the oscilloscope
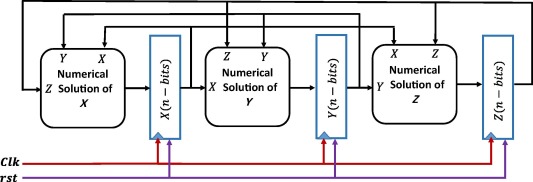
FPGA implementation of two fractional order chaotic systems
This paper discusses the FPGA implementation of the fractional-order derivative as well as two fractional-order chaotic systems where one of them has controllable multi-scroll attractors. The complete hardware architecture of the Grünwald-Letnikov (GL) differ-integral is realized with different memory window sizes. As an application of the proposed circuit, a complete fractional-order FPGA implementation of Liu chaotic system is introduced with different fractional-orders. Moreover, a fractional-order controllable heart and V-shape multi-scrolls chaotic systems are verified in the case of
Pagination
- Previous page ‹‹
- Page 31
- Next page ››
