CMOS realization of all-positive pinched hysteresis loops
Two novel nonlinear circuits that exhibit an all-positive pinched hysteresis loop are proposed. These circuits employ two NMOS transistors, one of which operates in its triode region, in addition to two first-order filter sections. We show the equivalency to a charge-controlled resistance (memristance) in a decremental state via detailed analysis. Simulation and experimental results verify the proposed theory. © 2017 B. J. Maundy et al.
Modelling supercapacitors leakage behaviour using a fractional-order model
A fractional-order circuit model is explored to represent the leakage/self-discharge behaviour of commercially available supercapacitors. This fractional order-model is composed of two elements, a fractional-order capacitor with impedance Z = 1/CαSα and a parallel resistance Rp, which set the discharge based on the time constant τ = (RpC)1/α and order α. Self-discharging data was collected from a 3 F PowerStor, 1 F Panasonic, and 350 F Maxwell supercapacitors after being charged and left in a floating state while monitoring the device terminal voltage. The parameters for the fractional-order
Mathematical techniques of fractional order systems : A volume in advances in nonlinear dynamics and chaos (ANDC)
Mathematical Techniques of Fractional Order Systems illustrates advances in linear and nonlinear fractional-order systems relating to many interdisciplinary applications, including biomedical, control, circuits, electromagnetics and security. The book covers the mathematical background and literature survey of fractional-order calculus and generalized fractional-order circuit theorems from different perspectives in design, analysis and realizations, nonlinear fractional-order circuits and systems, the fractional-order memristive circuits and systems in design, analysis, emulators, simulation
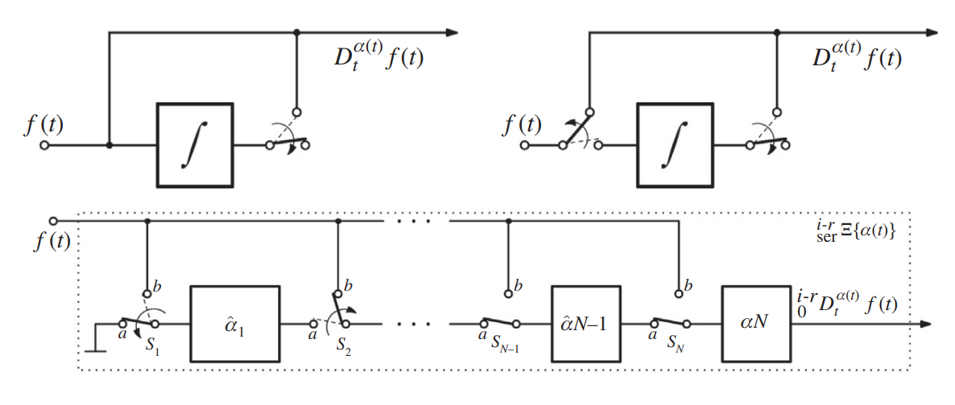
Conditions and Emulation of Double Pinch-off Points in Fractional-order Memristor
Recently, double pinch-off points have been discovered in some memristive devices where the I-V hysteresis curve intersects in two points generating triple lobes. This paper investigates a fractional-order flux-controlled mathematical model which is able to develop the multiple pinch-off points or multiple lobes. The conditions for observing double pinch-off points (triple lobes) are derived in addition to the locations of the pinch-off points which do not appear in the integer domain. Also, expressions for maximum and minimum conductance are derived. Finally, a floating fractional flux
True random bit generators based on current time series of contact glow discharge electrolysis
Random bit generators (RBGs) in today's digital information and communication systems employ a high rate physical entropy sources such as electronic, photonic, or thermal time series signals. However, the proper functioning of such physical systems is bound by specific constrains that make them in some cases weak and susceptible to external attacks. In this study, we show that the electrical current time series of contact glow discharge electrolysis, which is a dc voltage-powered micro-plasma in liquids, can be used for generating random bit sequences in a wide range of high dc voltages. The
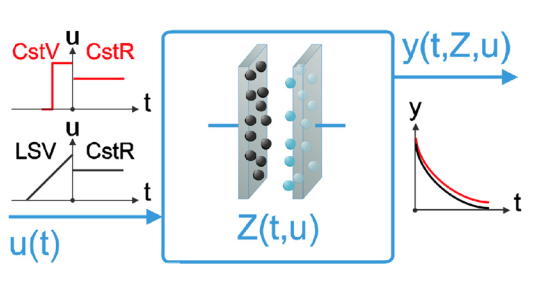
Short-term memory in electric double-layer capacitors
Shared by various physical, chemical, and biological systems, fractional-order dynamics assert that the present state of a system is the result of not only the applied stimulus but also its past history. Consequently, in fractional-order systems, there exists a system-specific, input-dependent memory kernel. In this study, we demonstrate experimentally the existence of a memory effect in electric double-layer capacitors which are known to exhibit a fractional-order behavior through their non-single, distributed internal time constants. This is performed by showing variance in the discharge
Simple MOS transistor-based realization of fractional-order capacitors
A new second-order MOS transistor based circuit block approximating the behavior of a fractional-order capacitor is proposed. The circuit is modular and therefore the order of the approximation can be increased by more stages of the same circuit in cascade or in parallel. Simulation results using a TSMC 65nm CMOS technology are provided and show less than 2o of phase error in two decades around the center frequency of the approximation. Experimental results of realized fractional-order capacitors and of a fractional-order relaxation oscillator are also shown. © 2019 IEEE
Comprehensive comparison based on meta-heuristic algorithms for approximation of the fractional-order Laplacian s α as a weighted sum of first-order high-pass filters
To implement an approximation of the fractional order Laplacian operator s α as a weighted sum of high pass filter sections, it is essential to extract the cutoff frequencies and filter gains of each section in order to achieve the lowest error possible. Therefore, in this work, five meta-heuristic optimization algorithms are tested in this problem based on a weighted sum objective function. The employed algorithms include the: ant-lion optimizer, cuckoo search algorithm, flower pollination algorithm, whale optimizer, and multi-verse algorithm. A comparison is carried out between the results
Fractional-order electric double-layer capacitors with tunable low-frequency impedance phase angle and energy storage capabilities
In this study, we report the electrical response of two sets of solid-state fractional-order electrochemical capacitors for which the low-frequency impedance phase angle can be tuned from - 69 ° to - 7 °. The configuration makes use of a gel electrolyte in which carbonaceous additives (graphite or reduced graphene oxide) are dispersed at different proportions. Such a disordered electrolyte structure results in subdiffusive charge transport and thus a frequency dispersive capacitive-resistive behavior typical of a constant phase element, which can be useful for both frequency applications and
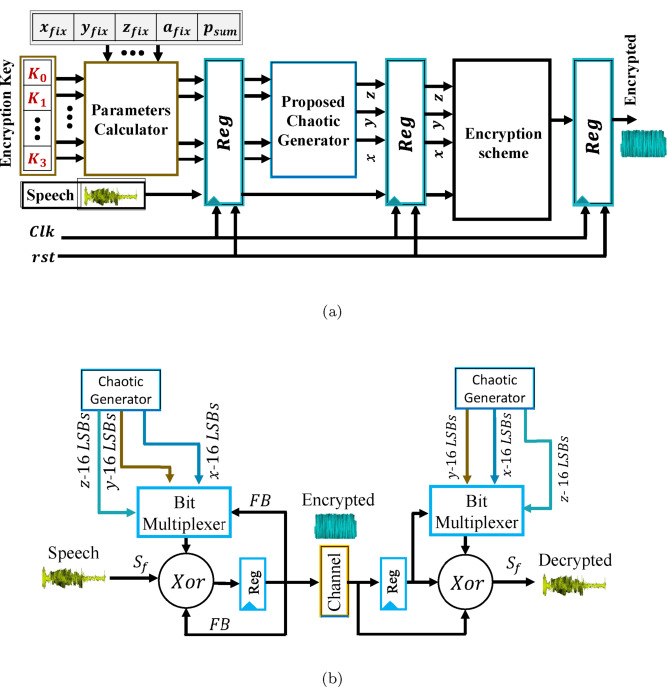
FPGA implementation of a chaotic oscillator with odd/even symmetry and its application
We propose a mathematical system capable of exhibiting chaos with a chaotic attractor which is odd symmetrical in the x − y phase plane but even symmetrical in the x − z and y − z phase planes respectively. A hardware implementation of the system is done on a digital FPGA platform for verification. The system is also attractive in the sense that (i) its dynamics are single-parameter controlled and (ii) it inherently generates two chaotic clock signals. As an application, an FPGA design methodology using this oscillator for speech encryption is demonstrated. The security of the proposed
Pagination
- Previous page ‹‹
- Page 37
- Next page ››
