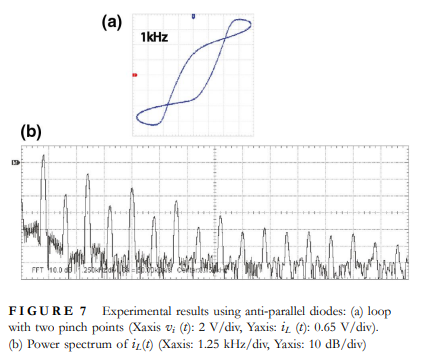
Pinched hysteresis loops in non-linear resonators
This study shows that pinched hysteresis can be observed in simple non-linear resonance circuits containing a single diode that behaves as a voltage-controlled switch. Mathematical models are derived and numerically validated for both series and parallel resonator circuits. The lobe area of the pinched loop is found to increase with increased frequency and multiple pinch points are possible with an odd-symmetrical non-linearity such as a cubic non-linearity. Experiments have been performed to prove the existence of pinched hysteresis with a single diode and with two anti-parallel diodes. The
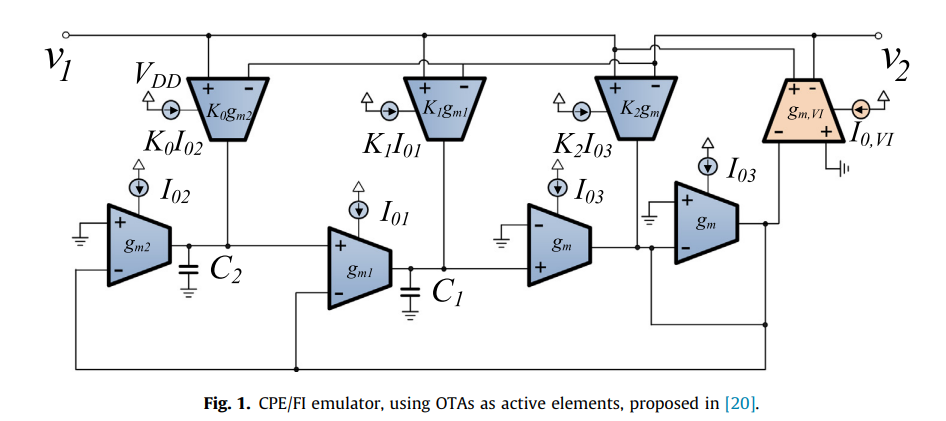
Low-voltage and low-power fractional-order parallel tunable resonator
A novel implementation of a fractional-order parallel resonator, capable of operating in a ±0.5 V power supply voltage environment, is presented in this work. Compared to the corresponding already published structures, it offers the benefit of reduced circuit complexity, due to the utilization of very simple voltage-mode 1st-order filter sections, leading also to reduction in the dc power consumption. Electronic tuning capability is another attractive feature of the proposed structure achieved using programmable MOS transistor transconductance parameters. © 2019 Elsevier Ltd
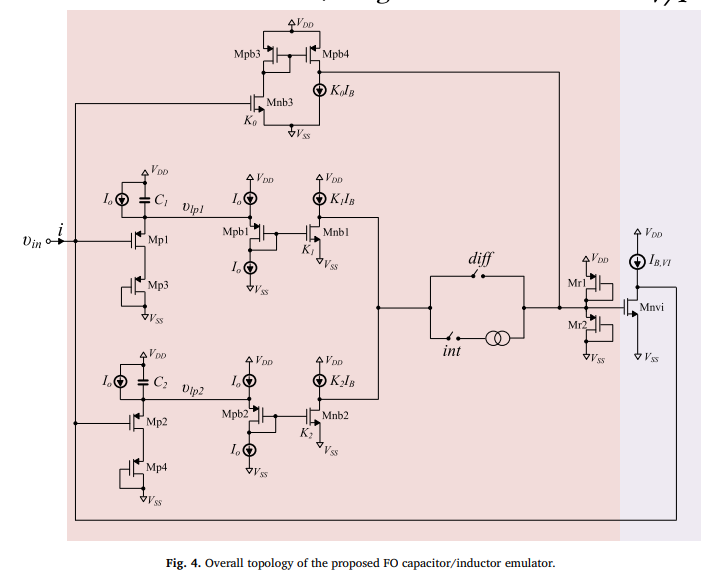
One-terminal electronically controlled fractional-order capacitor and inductor emulator
A novel topology for simultaneous emulation of fractional-order capacitors and inductors is presented in this paper. In particular, only one control terminal is used in order to select the type of the element as well as its fractional order. This is achieved through an appropriate fitting of the expressions of the intermediate bias currents, in such a way that, eventually, only the adjustment of one main bias current is required. The performance of the proposed topology is evaluated through post-layout simulations using Cadence and Austria Mikro Systeme (AMS) 0.35μm CMOS process. © 2019
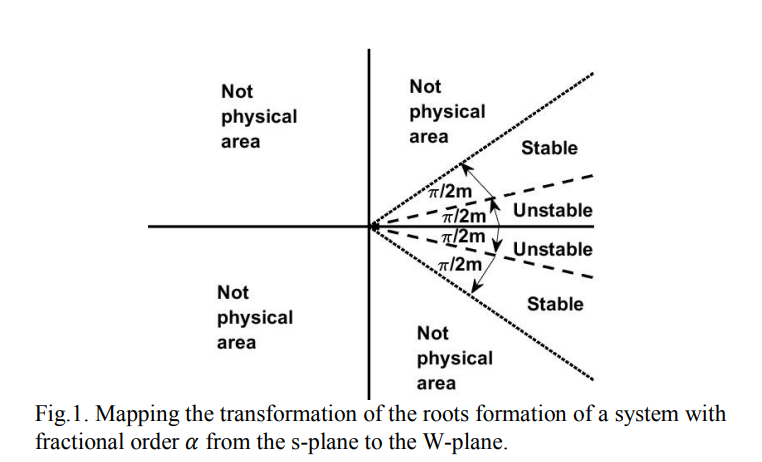
Generalization of third-order low pass filters to the fractional-order domain with experimental results
This paper is concerned with the generalization of continuous-time 3rd order low-pass filters to the fractional order domain. Three fractional-order capacitors of the same order α are to be considered in the process of filter design. A complete mathematical analysis of the 3rd order fractional low-pass filter is given with stability constraints taken into consideration. Finally, several low-pass active filter design examples are illustrated and discussed in the simulations section in terms of numerical MATLAB simulations, PSpice simulations and experimental results. © 2018 IEEE.
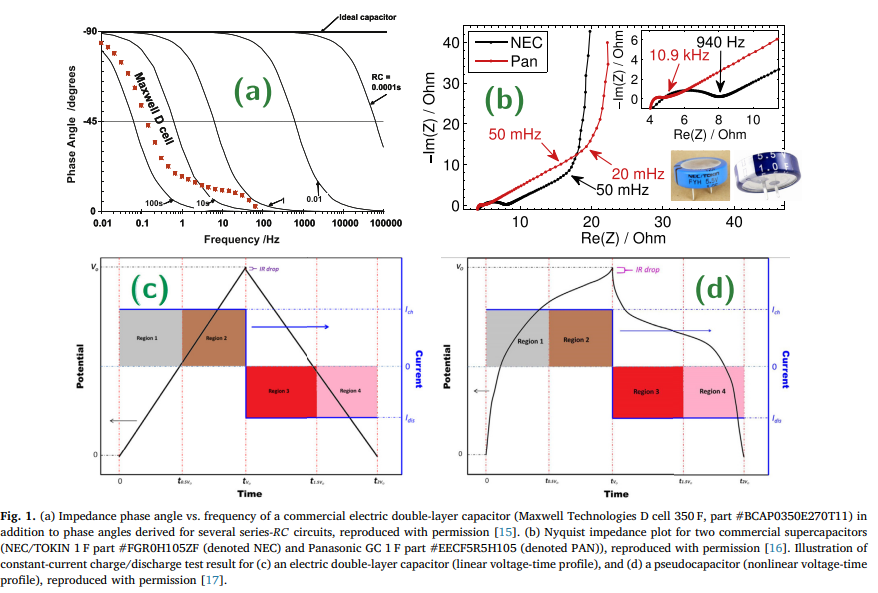
Review of fractional-order electrical characterization of supercapacitors
The tests and calculation of the key performance metrics of supercapacitors including capacitance, power and energy stored are commonly reported by the academia and the industry based on formulæ valid only for ideal capacitors. This is inconsistent with the fact that supercapacitors exhibit electrical behaviors that are different from those of ideal capacitors whether they are looked at in the time domain or in the frequency domain. This results inevitably in errors in their characterization, design and system integration. Based on recent literature, this review article is an attempt to
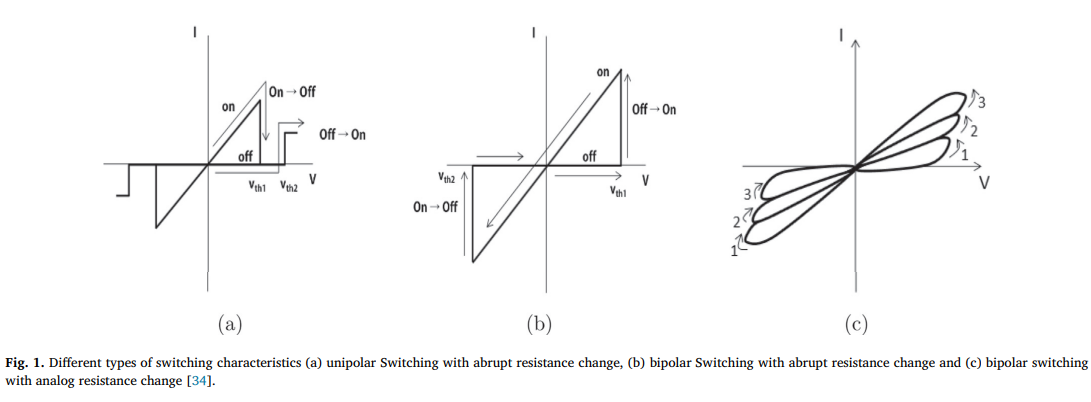
Design and analysis of 2T2M hybrid CMOS-Memristor based RRAM
In this paper, a Static Noise Margin (SNM) analysis for 2T2M RRAM cell is investigated. The proposed analysis is done using mathematical formulation and verified by SPICE simulations. The analysis is tested for both, write and read modes. Moreover, the analysis is applied to diverse types of RRAM cells, and a comparison between the performance of such cells is discussed. Additionally, the effect of the exponential memristor model on the memristor behaviour in terms of switching speed and the range of the memristor resistance are discussed in detail. The circuits design and simulations were
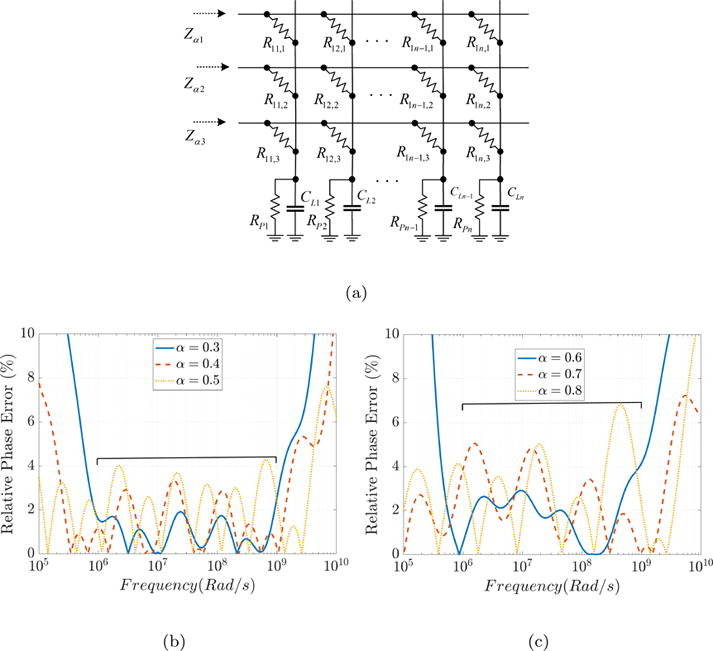
Programmable constant phase element realization with crossbar arrays
Introduction: Constant Phase Elements (CPEs) have been widely used in many applications due to the extra degree of freedom, which offers new responses and behaviors. Objectives: This paper proposes a new programmable CPE realization using resistive crossbar arrays. By programming the resistive devices, different CPEs can be obtained. Methods: The proposed realization can be approximated as a weighted sum of low and high pass filters having the same cut-off frequency (i.e., Lapicque model). The closed-form approximation expression is derived, and then the Flower Pollination Algorithm (FPA) is
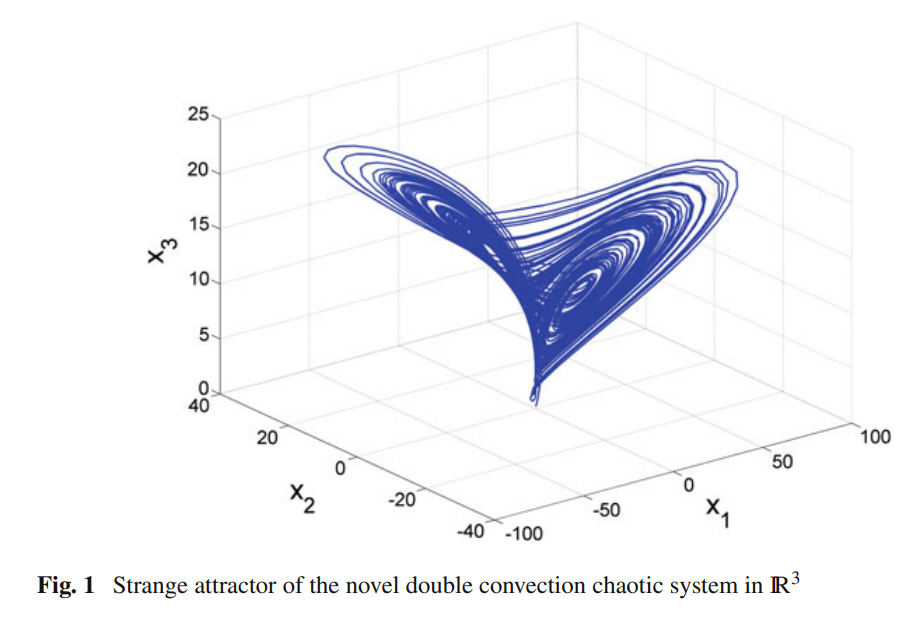
Adaptive control of a novel nonlinear double convection chaotic system
This researchwork describes a six-term novel nonlinear double convection chaotic system with two nonlinearities. First, this work presents the 3-D dynamics of the novel nonlinear double convection chaotic system and depicts the phase portraits of the system. Our novel nonlinear double convection chaotic system is obtained by modifying the dynamics of the Rucklidge chaotic system (1992). Next, the qualitative properties of the novel chaotic system are discussed in detail. The novel chaotic system has three equilibrium points. We show that the equilibrium point at the origin is a saddle point

Adaptive control of a novel nonlinear double convection chaotic system
This research work describes a six-term novel nonlinear double convection chaotic system with two nonlinearities. First, this work presents the 3-D dynamics of the novel nonlinear double convection chaotic system and depicts the phase portraits of the system. Our novel nonlinear double convection chaotic system is obtained by modifying the dynamics of the Rucklidge chaotic system (1992). Next, the qualitative properties of the novel chaotic system are discussed in detail. The novel chaotic system has three equilibrium points. We show that the equilibrium point at the origin is a saddle point
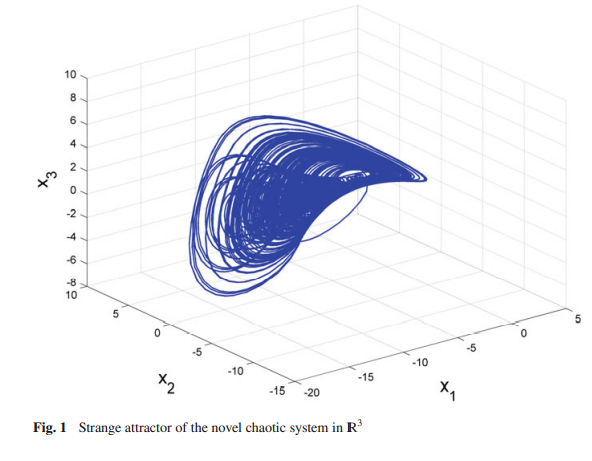
An eight-term 3-D novel chaotic system with three quadratic nonlinearities, its adaptive feedback control and synchronization
This research work describes an eight-term 3-D novel polynomial chaotic system consisting of three quadratic nonlinearities. First, this work presents the 3-D dynamics of the novel chaotic system and depicts the phase portraits of the system. Next, the qualitative properties of the novel chaotic system are discussed in detail. The novel chaotic system has four equilibrium points. We show that two equilibrium points are saddle points and the other equilibrium points are saddle-foci. The Lyapunov exponents of the novel chaotic system are obtained as L1 = 0.4715, L2 = 0 and L3 = −2.4728. The
Pagination
- Previous page ‹‹
- Page 39
- Next page ››
