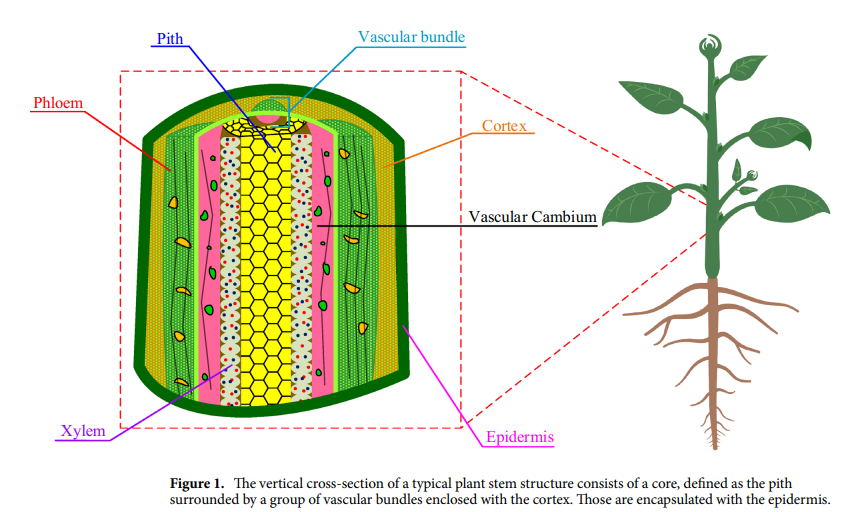
Sliding mode stabilization and synchronization of fractional order complex chaotic and hyperchaotic systems
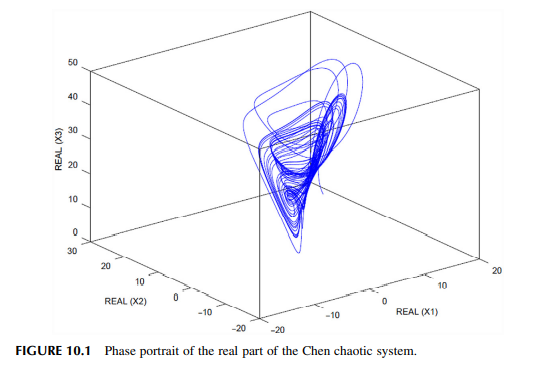
This chapter is intended to design and analyze several sliding mode techniques for the stabilization and synchronization of fractional order complex chaotic and hyperchaotic systems. Considering that chaos is a hot topic nowadays due to the vast number of real physical systems such as mechanical, electrical, and chemical systems in which this phenomenon is found; this book chapter will provide novel sliding mode approaches for the stabilization and synchronization of chaotic and hyperchaotic systems. Fractional order chaotic and hyperchaotic systems have been proved to be difficult to synchronize and stabilize so in order to achieve these objectives, several sliding mode approaches for fractional order systems are implemented such as adaptive sliding mode and terminal sliding mode. The first part of this book chapter is oriented to the stabilization of chaotic and hyperchaotic systems implementing a terminal sliding mode approach. The chaotic complex Chen system along with a hyperchaotic complex Lorenz attractor are used in this study. Then, in the second part of this book chapter the complex chaotic and hyperchaotic systems are synchronized with nonidentical and identical systems, respectively, implementing the adaptive terminal sliding mode control approach. To show the effectiveness of these approaches, several numerical simulation examples are provided along with a discussion and conclusion section. © 2018 Elsevier Inc. All rights reserved.